Un grupo de matemáticos presenta el viaje por carretera definitivo para visitar 50.000 lugares históricos de EE.UU.

• Calcularon el camino más corto para visitar 49.603 sitios históricos
• La mejor ruta de ida y vuelta tiene una longitud de 350.202 kilómetros
• William Cook, quien lideró el estudio, es un experto en el Problema del Agente Viajero

Los 49.603 lugares históricos de EE.UU. utilizados en la resolución del Problema del Agente Viajero.

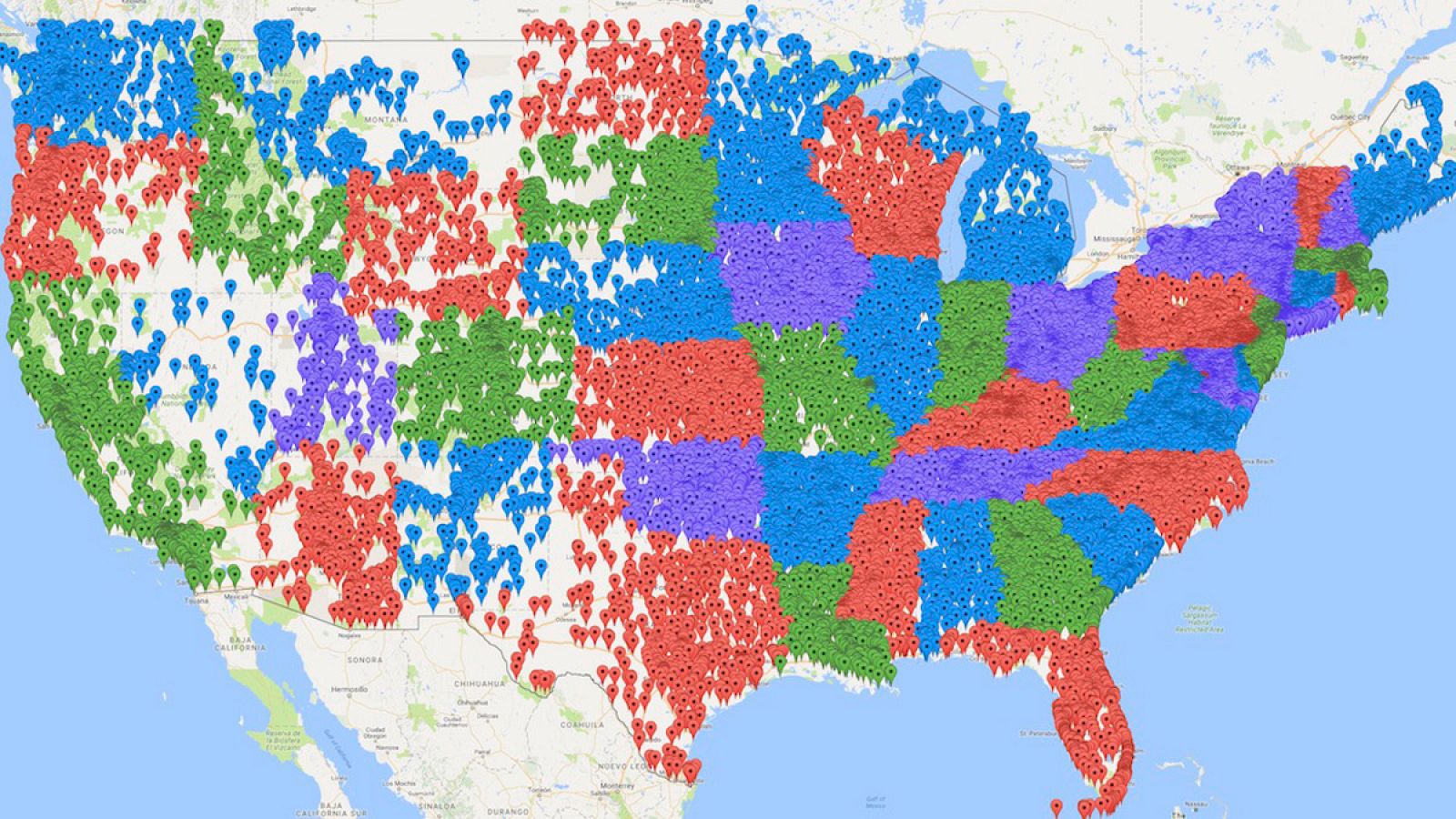
El profesor William Cook, de la Universidad de Waterloo (Canadá), ha liderado un equipo internacional que ha encontrado el camino más corto posible para visitar 49.603 lugares inscritos en el Registro Nacional de Sitios Históricos de Estados Unidos, diseñando de esta manera el que podría considerarse como el viaje por carretera definitivo.

Aunque el Registro de Sitios Históricos recoge más de 90.000 lugares, Cook seleccionó menos de 50.000. Además, el programa eliminó los sitios duplicados como hitos o puentes compartidos por diferentes estados.

Cook, quien ejerce la docencia en la Facultad de Matemáticas de Waterloo, es un experto en el Problema del Agente Viajero (TSP por sus siglas en inglés). El TSP se nos presenta cuando tenemos una lista de lugares y necesitamos encontrar la ruta más corta -de ida y vuelta- para visitar todos. Algo sencillo si la lista es corta pero que supone un auténtico desafío matemático si incrementamos su número exponencialmente.

"Nuestro objetivo no era planear las vacaciones definitivas de los apasionados de la historia", ha dicho Cook, sino "más bien, usamos los problemas de viajes como un medio para desarrollar y testar métodos de optimización, los cuales pueden ser útiles a la hora de encontrar la ruta más eficiente para camiones de reparto que llevan paquetes a tu puerta, programar los ciclos de producción en fábricas y otras aplicaciones en la industria, ciencia y comercio".

Partiendo de las coordenadas geográficas de los 49.603 sitios históricos y calculando la distancia entre dos puntos como la longitud de la ruta a pie hallada con Google Maps, se trataba de hallar la ruta más corta para pasar por todos ellos y volver al punto de partida.

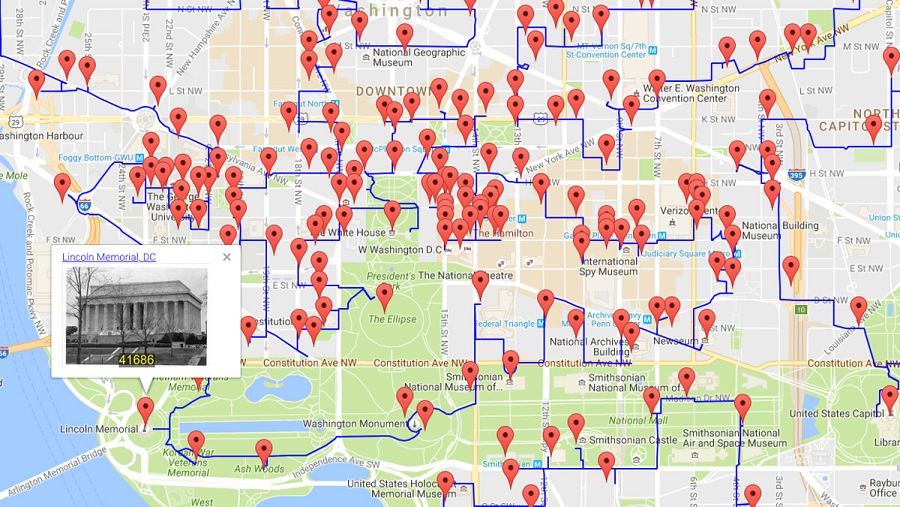
Washington. University of Waterloo

"No obstante, teníamos que asumir que la ruta que Google nos sugería para caminar entre dos puntos cualesquiera A y B no era más corta que la longitud de la ruta que un cuervo describiría en su vuelo. Debido a ello era posible concebir una solución sin tener que preguntar a Google por la distancia entre pares de puntos, algo a tener en cuenta ya que se trataba de 1.230.204.003 pares y Google tiene un límite de 2.500 requerimientos de distancia por día", explican desde la Universidad de Waterloo.

La resolución al problema requirió del uso de 310 ordenadores entre los pasados meses de marzo y noviembre. El tiempo computacional total, sumando la contribución de todos los procesadores, fue de 178,9 años.

El tour óptimo cubre una distancia de 350.201,525 kilómetros, unas 217.605 millas, lo cual equivale a algo menos de la distancia entre la Tierra y la Luna. "No existe un tour alternativo que sea tan siquiera un metro más corto que el producido por nuestra computación", concluyen.

Anteriormente, "a modo de calentamiento", el mismo equipo había calculado la ruta más corta para recorrer 24.727 pubs en el Reino Unido. No obstante, resolver ese problema solo requirió 0,8 años computacionales.