Descubren un nuevo principio matemático que puede ayudar a entender cómo se forman los órganos

• El estudio publicado en Cell Systems significa un paso importante para la creación de tejidos y órganos artificiales
• El modelo biofísico tiene su origen en un artículo de 2018 y pone la clave en las 'relaciones sociales de las células'

Tejido donde las células epiteliales forman un tubo

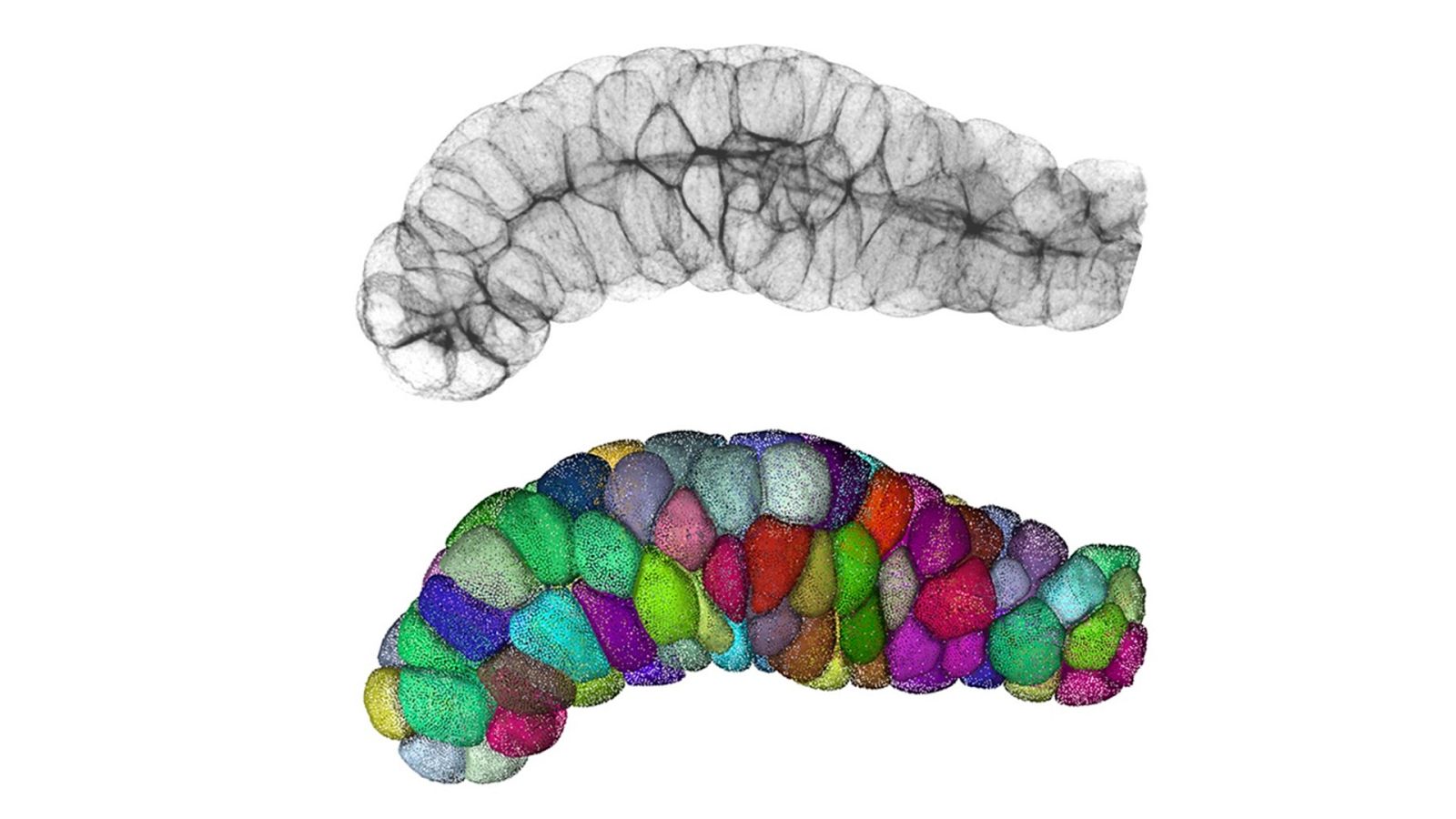
Un nuevo principio matemáticodescubierto por un equipo científico internacional podría ayudar a entender cómo se forman los órganos durante el desarrollo embrionario al explicar cómo se conectan las células entre sí para formar los tejidos.

El trabajo, publicado en la revista Cell Systems, ha utilizado la mosca de la fruta como modelo y, de acuerdo a los investigadores, sería un paso importante para futuras implicaciones en la creación de tejidos y órganos artificiales, "un gran reto para la biología y la biomedicina".

El hallazgo ha sido anunciado este miércoles por el Consejo Superior de Investigaciones Científicas (CSIC), cuyos institutos de Biología Integrativa de Sistemas (I2SysBio) y de Biomedicina de Sevilla (IBiS) han liderado el estudio.

Han participado, además, la Universitat de València el Hospital Universitario Virgen del Rocío, la Universidad de Sevilla, la Universidad Johns Hopkins de Estados Unidos y la Universidad del País Vasco, entre otras instituciones.

Un modelo biofísico que se remonta a 2018

El mismo grupo de investigadores que ha hallado el nuevo principio matemático ya hizo público en Nature Comunications (2018) un artículo que tuvo un gran impacto científico y mediático. En él, los científicos probaron que las células epiteliales pueden adoptar una forma geométrica durante la formación de los órganos que no estaba descrita hasta ese momento: el escutoide.

Dicho descubrimiento supuso un importante cambio de paradigma. Hasta entonces, los epitelios siempre se habían estudiado usando conceptos matemáticos para describir su organización en dos dimensiones, algo que está relacionado con la conexión entre las células y cómo se comunican entre ellas para formar esos órganos correctamente. "Sin embargo, como demostramos, las células epiteliales pueden tener formas complejas en tres dimensiones, como los escutoides, y las células y los órganos también son tridimensionales", explica uno de los autores, Luisma Escudero.

Ahora, el nuevo artículo ha dado un paso más al plantearse si existen principios matemáticos y/o biofísicos en 3D y al elaborar "un modelo biofísico que relaciona por primera vez la geometría del tejido y las propiedades físicas de las células con cómo están conectadas entre sí".

Las 'relaciones sociales' de las células, la clave del estudio

El antropólogo Robin Dunbar determinó que los seres humanos tenemos un promedio de cinco amigos íntimos que vienen dados por diferentes factores sociales y personales y, a nivel celular, el artículo ha desvelado un principio equivalente, como detalla el colíder del estudio Javier Buceta. "El número de vecinos próximos de una célula, es decir, sus amigos íntimos, está determinado en este caso por la geometría del tejido y sus relaciones energética", añade respecto al símil.

“Así, teniendo en cuenta una serie de consideraciones energéticas, biológicas y geométricas, hemos descubierto que, por ejemplo, cuantas más conexiones tiene una célula epitelial con otras, más energía necesita para establecer nuevas conexiones con otras células, mientras que, si está poco conectada con otros vecinos, la célula necesita menos energía para establecer ese vínculo”, destaca Buceta.

Para descubrir esto, los científicos alteraron el tejido, reduciendo la adhesión entre las células para poner su modelo a prueba: "Esto hace que cambie la organización, al ser más fácil, menos costoso, energéticamente hablando, que las células contacten con nuevas células". Los resultados de los experimentos confirmaron el principio cuantitativo propuesto.

Por tanto, los resultados muestran cuantitativamente cómo la geometría de los escutoides condiciona la conectividad celular y cómo pueden ser un instrumento biológico para regular las propiedades, como material, de tejidos y órganos.