¡Paradojas, fractales, ecuaciones y patitos de goma a la deriva! Matemáticas en mares revueltos, por Clara Grima

• ¿Hay matemáticas en el mar? Muchísimas. Paradojas, patitos de goma a la deriva y otras ecuaciones sin resolver, por Clara Grima
• Una matemática viene a verte: Todos los miércoles, en La 2 a las 19:45 horas | Disponible en RTVE Play

Patito de goma en el mar

Que las matemáticas están en (casi) todo lo que hacemos es un hecho que no por mucho repetirse deja de ser cierto. Algunas veces se descubren con mucha facilidad al mirar un extracto bancario o la imponente belleza de un edificio y otras veces se esconden, o parece que tratan de hacerlo, en paisajes menos cuantificables, nada geométricos (en apariencia).

Las matemáticas del mar

Se acerca el ¿buen? tiempo y muchos de nosotros nos sentaremos frente al mar, para dejar que nuestros pensamientos bonitos se mezan con las olas y esperando que estas mismas arrastren nuestras preocupaciones a lo más profundo del azul.

Pero, ¿hay matemáticas en el mar?

Muchísimas. Casi de cualquier rama de esta disciplina que se nos ocurra. Por ejemplo, ¿cuántas estrellas habrá en el fondo del mar? No disponemos, hasta donde yo sé, de este dato, pero les animo a que hagan una estimación del mismo y me la cuenten en Twitter.

Si le preguntan a casi cualquier matemática que vaya a verle qué matemáticas esconde el mar, posiblemente, entornará los ojos unos segundos para pensar y les contará alguna de estas dos.

Puede que lo primero que le venga a la cabeza sea la costa británica y Benoit Mandelbrot (ilustre matemático franco-americano, nacido en Polonia). Sí, porque fue tratando de calcular cuánto medía la costa británica como, en 1967, cuando nuestro querido Benoit intuyó la existencia de unos objetos matemáticos que no habían sido descritos aún, situados en la frontera que separa el orden del caos, tan bellos como enigmáticos: los fractales.

Benoit Mandelbrot planteó la siguiente, en principio, paradoja: cuanto más pequeña sea la unidad de medida usada para medir la costa, más medirá esta. La siguiente imagen nos aclara mejor lo que quiero decir:

Medir la costa Británica

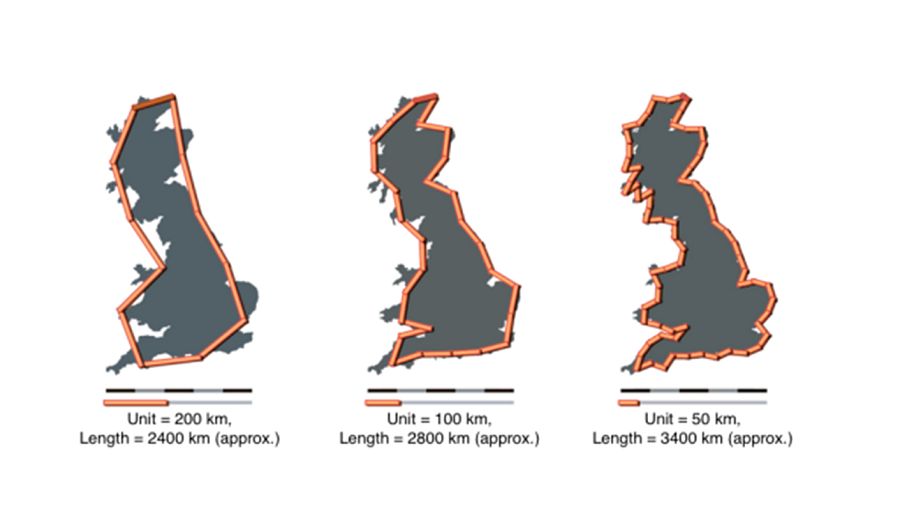
Diferentes unidades de medida para la Costa Británica Wikipedia

Si usamos (para medir la costa) una ‘regla’ de 200 km, nos salen unos 2400 km de costa británica. Si la regla es de 100 km, la costa mide unos 400 km más. Sí, como lo leen. Pero si nuestra ‘regla’ es de 50 km, ojo, la costa británica mide aproximadamente 3400 km, mil kilómetros más que con la regla de 200 km. ¿Qué magia es esta?

A partir de esta ‘magia’, Benoit Mandelbrot intuyó, como ya hemos dicho, que existían objetos geométricos que las matemáticas aún no habían sabido describir. Observó además que estos objetos, los fractales eran autosimilares, o lo que es lo mismo, que si tomábamos un trozo de ellos y hacíamos zoom sobre él, nos acercábamos lo suficiente, volveríamos a encontrar esa misma forma (la del trozo) repetida una infinidad de veces.

Triángulo de Sierpinski

Triángulo de Sierpinski WIKIPEDIA

Los fractales son uno de los temas estrella en la divulgación de las matemáticas, hay ilustraciones maravillosas de algunos de ellos y, actualmente, son una herramienta muy interesante en la detección de enfermedades como el cáncer. No descarten que muy pronto profundicemos más sobre fractales pero hoy nos vamos a sumergir en otras matemáticas del mar.

Patitos viajeros

Viajamos en el tiempo, hasta enero de 1992, y en el espacio (al menos yo, desde Sevilla) hasta el Océano Pacífico. Fue allí donde un barco, el "Evergreen Ever Laurel", que navegaba de Hong Kong a Tacoma (Washington) desparramó, por accidente, 29 000 juguetes de plástico que, 10 meses después, aparecieron en Sitka (Alaska). Más tarde fueron apareciendo patitos de goma en Japón, Indonesia, Australia, Nueva Zelanda y América del Sur.

Patitos de goma a la deriva

Patitos de goma GETTY

¿Qué tienen que ver los patitos viajeros con las matemáticas?

Muchísimo. De hecho, en mayo de 2021, un grupo de matemáticos españoles (Eva Miranda, Robert Cardona, Daniel Peralta y Francisco Presas) publicaron un artículo en en PNAS (Proceedings of the National Academy of Sciences), una de las revistas científicas más importantes del mundo abordando este naufragio. El problema (matemático) que trataban de abordar Eva y sus colegas tenía que ver con el mar y los patitos en tanto que estaban interesados en decidir si sería posible predecir el comportamiento de un fluido. Concretamente, el comportamiento de las corrientes marinas. Les adelanto que la respuesta es negativa. Era imposible saber dónde irían a atracar los patitos.

Se podría pensar que, bueno, no es una gran tragedia para la humanidad no saber cómo se comportan las corrientes marinas en general. Toda vez que el ser humano ha desarrollado herramientas suficientemente potentes y efectivas para llevar a los patitos (o lo que sea) donde haga falta. Si es que nuestra ciencia y nuestra tecnología ya pueden con todo. O con casi todo.

Previsiones metereológicas

¿Saben, por ejemplo, que a causa de la pandemia las previsiones meteorológicas son menos fiables? Desde hace mucho tiempo se conocen perfectamente las ecuaciones matemáticas que rigen la meteorología: las ecuaciones de la dinámica de fluidos (también la dinámica de los patitos en el mar) y de la termodinámica. Son las ecuaciones de Navier-Stokes. Pero aunque estas ecuaciones se escribieron en el siglo XIX nuestra comprensión de ellas sigue siendo mínima. No sabemos ni resolverlas ni intuir si las soluciones serán estables en el tiempo (y buenas para hacer predicciones) o caóticas (con cambios bruscos, impredecibles). Efectivamente, resolver las ecuaciones de Navier-Stokes es otro de los Problemas del Milenio, como P vs NP.

Pues bien, en estos casos, en los que no se pueden resolver las ecuaciones de forma exacta, lo que hacemos son muchísimas, pero muchísimas, simulaciones numéricas que nos puedan dar una aproximación fiable de la solución exacta. Durante el confinamiento se suspendieron muchísimos vuelos comerciales y eran estos vuelos, principalmente, los sensores utilizados para recopilar los datos climatológicos en los distintos puntos del planeta. Menos datos, menos simulaciones, peor previsión meteorológica.

Como pueden ver, no podemos predecir con certeza ni las corrientes marinas ni el tiempo meteorológico. Pero cada vez lo hacemos mejor. Sobre esto último, sobre previsiones meteorológicas a corto, medio y, sobre todo, largo plazo hablaremos en el tercer programa de Una matemática viene a verte con Silvia Laplana y Juan Pedro Montávez.

Nos vemos en La 2.

* Puedes disfrutar del programa Una matemática viene a verte cada miércoles a las 19:45 horas en La 2 y siempre, cuando quieras -gratis y online- en RTVE Play.