Triaungulación en matemáticas: ¿Cómo los números dan vida a mundos virtuales asombrosos?

• Jugando con triángulos, Clara Grima detalla algunos de los cálculos matemáticos que hay en los videojuegos
• Una matemática viene a verte: Todos los miércoles, en La 2 a las 19:45 horas | Disponible en RTVE Play

Una matemática viene a verte - Programa 5: Súper Matemáticas Bros

Cuando se habla de matemáticas, un porcentaje nada despreciable de la población se refiere a ellas como ciencias exactas. Y lo son, casi siempre. Cuando pueden serlo, claro. Porque en ocasiones debemos conformarnos con aproximaciones. Y, francamente, no nos va tan mal.

Si han seguido los programas de Una matemática viene a verte, cosa que les recomiendo fuertemente, sabrán que, a día de hoy, es imposible diseñar una gira óptima para un cantante, si la ruta incluye muchas ciudades.También que es imposible, a día de hoy, hacer una previsión exacta del tiempo meteorológico o resolver problemas de organización y empaquetamiento en la cocina de un restaurante. Por ejemplo. En todos esos casos, y en muchos otros, como he dicho, lo que hacemos es tratar de encontrar buenas aproximaciones a la solución del problema, porque no podemos aspirar a encontrar la exacta (nos llevaría demasiado tiempo). Por ahora.

Pero, como digo, hay otras situaciones, muchas, en las que, a falta del dato exacto, las matemáticas nos ayudan a calcular el valor aproximado de un dato desconocido, por ejemplo, porque no se midió.

Más concretamente. Vamos a imaginar que queremos representar una determinada zona geográfica en una imagen 3D para, por ejemplo, un videojuego. Queremos que la representación sea lo más fiel posible a ese cerro que está en nuestro pueblo de la infancia porque nos evoca recuerdos dulces y con olor a colonia infantil.

Para ello, nos hacemos de un taquímetro topográfico, y medimos la altura (sobre el nivel del mar) de los puntos del cerro, para darle esta información a nuestro ordenador y que este represente la superficie. La idea es fantástica pero una mijita inviable. No podemos medir la altura en todos los puntos del cerro porque sería tedioso y, si la nostalgia nos diese fuerza para medir en todos los puntos, serían demasiados datos.

¿Cómo lo hacemos entonces?

Una buena solución consiste en medir solo en algunos puntos del cerro y aproximar la altura de los que no hemos medido, usando matemáticas, claro.

Por ejemplo, imaginen que hemos medido la altura en 3 puntos que, en un alarde de imaginación, hemos etiquetado como A, B y C. Ahora queremos estimar la altura de un punto, el punto P, en el que no hemos medido: el punto azul que hemos dibujado en esta figura:

Baricéntricas

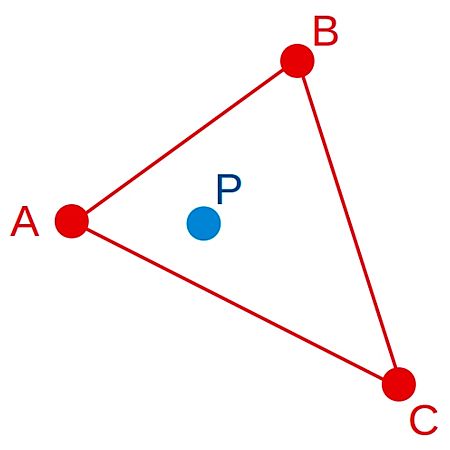
Baricéntricas RTVE

Para ello, usaremos interpolación baricéntrica. Les cuento cómo.

Si tenemos un triángulo formado por los vértices A, B y C, para cualquier punto de ese triángulo, P, se pueden calcular sus coordenadas baricéntricas respecto de A, B y C. Estas coordenadas baricéntricas serán 3 números, α, β y γ, que suman 1, y que cumplen que (en términos de coordenadas):

P= α.A + β.B + γ.C

Es decir, las coordenadas de P (latitud y longitud) se pueden escribir como α por las coordenadas de A, más β por las coordenadas de B, más γ por las coordenadas de C.

Pues bien, si son esas las coordenadas de P en el triángulo y conocemos la altura en A, h(A), en B, h(B) y en C, h(C), podemos dar una aproximación de la altura del terreno en P usando la siguiente fórmula:

h(P)= α.h(A) + β.h(B) + γ.h(C)

Ya tenemos una aproximación de la altura de P sin necesidad de volver al cerro a medir. Un momento. Para poder fiarnos de esa aproximación de la altura de P hay que comprobar algunas cosas más. Si solo conocemos la altura en 3 puntos (como en nuestro ejemplo), vale, no hay otros triángulos posibles para usar la interpolación, pero si hay más puntos las cosas cambian.

Vamos a fijarnos en el siguiente ejemplo: en ambos casos, hemos medido la altura en los puntos amarillos, usando un taquímetro, y en ambos casos, hemos construido triángulos con vértices en los puntos para los que conocemos su altura, los hemos triangulado, hemos hecho una triangulación de los puntos amarillos.

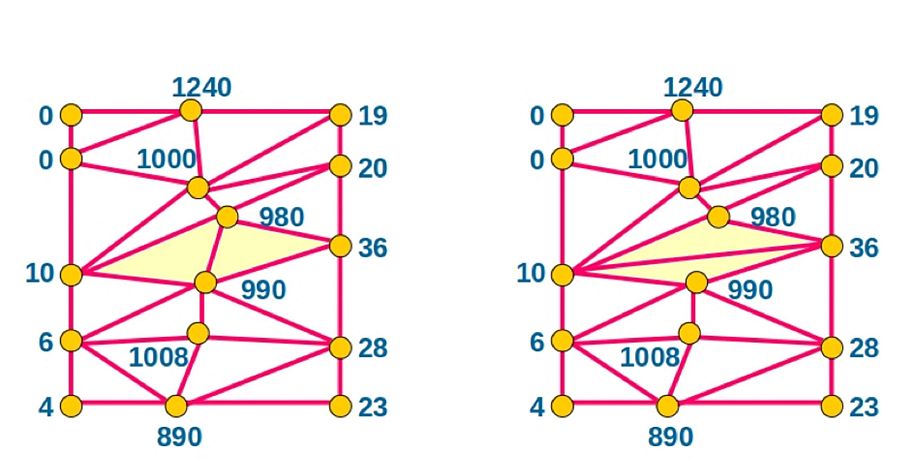
Ejemplo triangulación matemática RTVE

Si ahora, usando interpolación baricéntrica, queremos saber la altura del punto rojo, observamos que, depende de la triangulación que elijamos, nos da un resultado. Y sí, son muy diferentes.

triangulación matemática

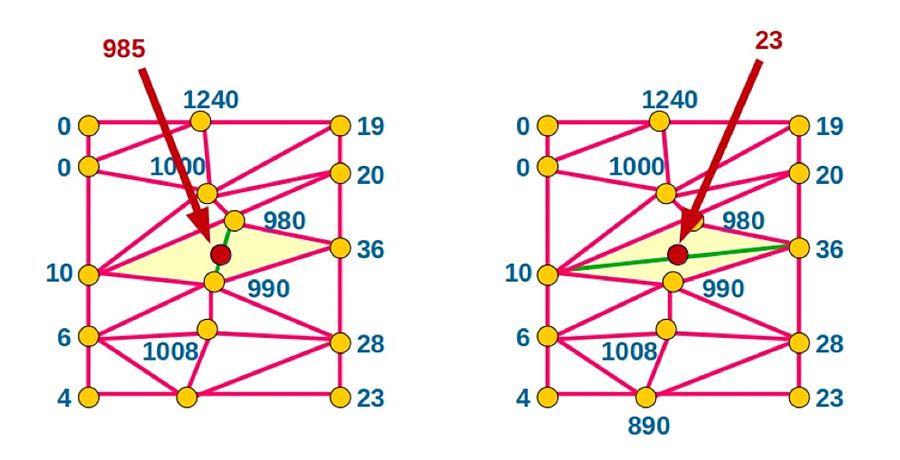
Ejemplo triangulación matemática RTVe

¿Qué ha pasado aquí?

El sentido común nos empuja a pensar que la mejor aproximación es la de 985 metros. En el otro caso, si entre 2 puntos a 980 y 990 metros hubiese un punto a una altura de 23 metros, un desnivel muy pronunciado en el terreno, habríamos medido su altura, para poder dar una representación más fiel del terreno e indicar la existencia de una depresión. Podemos deducir que si no hemos medido la altura en el punto rojo es porque no nos pareció relevante.

Concluimos, entonces, que la mejor triangulación es la de la izquierda.

¿Qué tiene esta triangulación mejor que la otra?

Tiene ángulos más grandes, triángulos más redonditos. Las dos triangulaciones son casi iguales, pero donde no lo son, la triangulación de la izquierda tiene triángulos con ángulos más grandes.

Por lo tanto, para modelizar un terreno digitalmente, ya tenemos el algoritmo. Medimos en algunos puntos, triangulamos bien esos puntos y para el resto, calculamos la altura usando interpolación baricéntrica en el triángulo en el que haya caído. Gráficamente, se puede pensar como que dibujamos los puntos (aquellos en los que medimos) en un plano (nos olvidamos de la 3ª coordenada, la que nos da la altura); triangulamos esos puntos en el plano y por último, los levantamos a la altura que sabemos que tienen, levantando los triángulos a la vez y obteniendo un modelo aproximado del terreno real.

Alzado

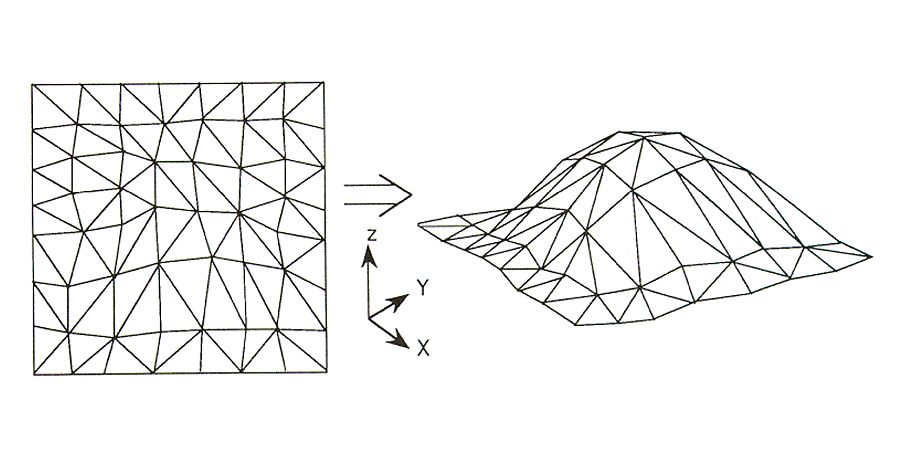
Alzado RTVE

El punto delicado es que, para podernos fiar de este modelo, la triangulación, como hemos dicho antes, tiene que ser buena. De hecho, queremos hacerlo con la mejor triangulación posible en el sentido que hemos dicho, la que tenga mejores (mayores) ángulos, la que tenga los triángulos más redonditos. A esta triangulación se le conoce con el nombre de triangulación de Delaunay.

A primera vista, esto puede agobiar porque en un primer acercamiento, uno puede pensar: “¿Tengo que calcular todas las triangulaciones distintas posibles y medir los ángulos de todas ellas?”

No, no hace falta. Hay algoritmos muy eficientes para calcular la triangulación de Delaunay de un conjunto de puntos sin necesidad de generar todas.

Dealunay 1

Ejemplo Dealunay 1 RTVE

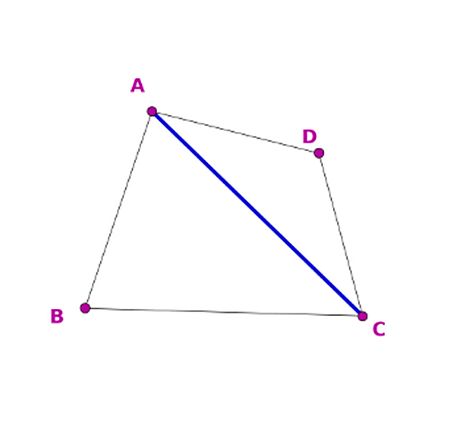
Por ejemplo, hacemos una triangulación de los puntos a nuestro antojo, sin preocuparnos de nada, simplemente, añadiendo segmentos (aristas) entre los puntos, de 2 en 2, sin que se crucen con los que ya están dibujados. Cuando no podamos añadir ninguno más, lo que nos queda es una triangulación. Ahora nos fijamos en una arista cualquiera interior, compartida por dos triángulos, y vamos a averiguar si dicha arista es de Delaunay.

En la figura siguiente, si nos fijamos en la arista AC, interior, esta es común a los triángulos ABC y ADC

Dealunay 2

Dealunay 2 RTVE

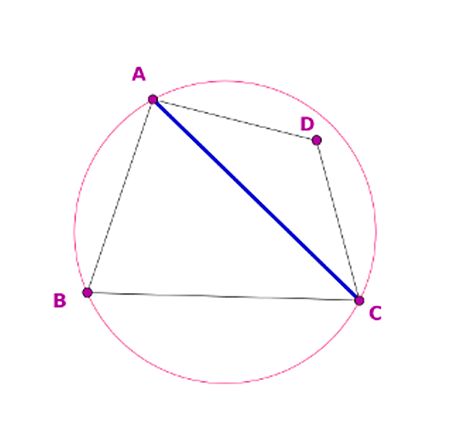
Dibujamos el círculo que pasa por los vértices de ABC (es único, 3 puntos no alineados determinan siempre un círculo) y comprobamos si el otro vértice,I (el del otro triángulo) está dentro del círculo.

Si está, como ocurre en nuestro ejemplo, sabemos que la arista AC no es de Delaunay, y la tenemos que cambiar por la BD, la otra diagonal del cuadrilátero ABCD. Esta operación se conoce como flip, en inglés, y aunque se traduce por giro o intercambio en castellano, lo cierto es que la mayoría de la comunidad de Geometría Computacional española, le llamamos flip e incluso conjugamos el verbo flipar. Somos así, no hay más.

Una vez hayamos hecho esto con todas las aristas interiores de nuestra triangulación, podemos estar seguros de que tenemos la triangulación de Delaunay y de que es la que mejor aproxima el relieve de nuestro amado cerro.

Hay infinidad de algoritmos que hacen esto, calcular la mejor triangulación posible, para conseguir mejores gráficos en nuestros ordenadores. Y este tipo de herramientas se usan habitualmente en el diseño de videojuegos.

De triángulos, matemáticas y videojuegos hablaron en Una matemática viene a verte, con Cristinini, José Céspedes de Pendulo Studios y Antonio J. Fernández Leiva, director de la Cátedra Videojuegos, Gamificación y Juegos Serios de la Universidad de Málaga.

* Puedes disfrutar del programa Una matemática viene a verte cada miércoles a las 19:45 horas en La 2 y siempre, cuando quieras -gratis y online- en RTVE Play.