Tengo unos dados (no transitivos) y no dudaré en ganarte. Cálculo de probabilidades, por Clara Grima

• Cómo manejar con soltura el cálculo de probabilidades, puede ayudarnos a ganar
• Una matemática viene a verte: Todos los miércoles, en La 2 a las 19:45 horas | Disponible en RTVE Play

Descubre cómo el cálculo de probabilidades desafía nuestra intuición en juegos de azar.

Nos encanta hablar de probabilidades. Vivimos en un mundo incierto y, en ocasiones, caótico. Nos gusta pensar (para nuestra tranquilidad) que sabemos manejar las probabilidades de los sucesos a la hora de tomar decisiones. Y esa es una buena filosofía, por supuesto, si los cálculos probabilísticos están bien hechos, claro.

La mala noticia es que, en general, somos muy malos haciendo esto mismo: evaluando probabilidades. Pero no hay que sentirse mal por ello, de ninguna manera. En primer lugar, porque son cálculos muy complicados en muchos casos. Y en segundo lugar porque, parafraseando a mi admirado Adrián Paenza, nadie es mejor ni peor por saber matemáticas.

De hecho, muchas veces, los cálculos de probabilidades ponen a prueba nuestra intuición. Un ejemplo muy claro de ello es la conocida paradoja del cumpleaños. Dicha paradoja nos asegura que la probabilidad de que en en un grupo de solo 23 personas, la probabilidad de que dos de ellas cumplan años el mismo día es mayor del 50%. “¿Cómo? ¿Con solo 23 personas? Pero si hay 365 (o 366) fechas distintas, ¡eso es imposible!”.

No, no lo es. Solo hay que hacer bien las cuentas. De hecho, si en el grupo hay 57 personas, la probabilidad de que dos de ellas cumplan años el mismo día es mayor del 99,666%.

Como digo, solo hay que hacer las cuentas. Y sí, es antiintuitivo, por eso se le llama paradoja. Pero no he venido a hablar de cumpleaños, ni de paradojas. Aunque sí de un juego de dados que reta también a nuestra intuición: los dados no transitivos.

No sé si recuerda de su época de estudiante que significa que una propiedad sea transitiva. En cualquier caso, se lo recuerdo con un ejemplo simple. Imaginemos que en unas elecciones el partido A obtiene más votos que el partido B; y que, a su vez, el partido B obtiene más votos que el partido C. En este caso, podemos asegurar que el partido A ha obtenido más votos que C. Puede que le haya parecido algo muy tonto y que haya pensado que esto ocurre con todas las propiedades pero no, no es así. Y vamos a ver un ejemplo, como le he dicho, con 3 dados no transitivos.

Dados con diferentes probabilidades de ganar RTVE

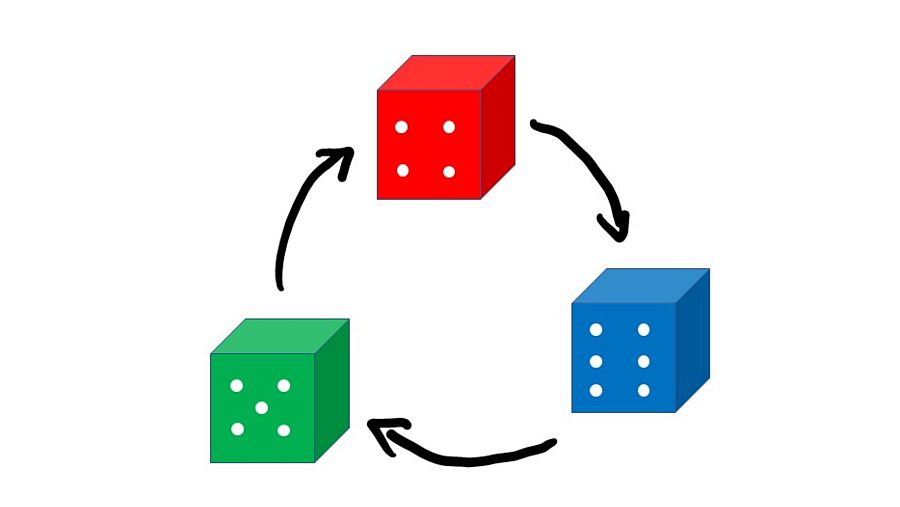
Nuestros dados no transitivos son los siguientes:

¿ El dado verde tiene 3 caras con 2 puntos y las otras 3 con 5 puntos.

¿ El dado rojo tiene 5 caras con 4 puntos y 1 cara con 1 punto.

¿ El dado azul tiene 5 caras con 3 puntos y 1 cara con 6 puntos.

Ahora le propongo un juego. Usted elige el dado que quiera y yo uno de los que descarte. Lanzamos por turnos nuestro dado y anotamos un punto a aquel de nosotros 2 que haya sacado más puntuación. Lo repetimos, por ejemplo, 25 veces. Gana el que más puntos haya acumulado al final. ¿Qué dado escogería? ¿Hay algún dado mejor que otro? Vamos a compararlos por parejas. Si usted elige el dado ROJO, yo elegiré el VERDE. ¿Por qué? Porque la probabilidad de que el dado VERDE saque más puntuación que el dado ROJO es más alta que la de que ocurra lo contrario. Vamos a verlo con una tabla de doble entrada, como esta, en la que hemos marcado los posibles resultados de cada uno de los 2 dados.

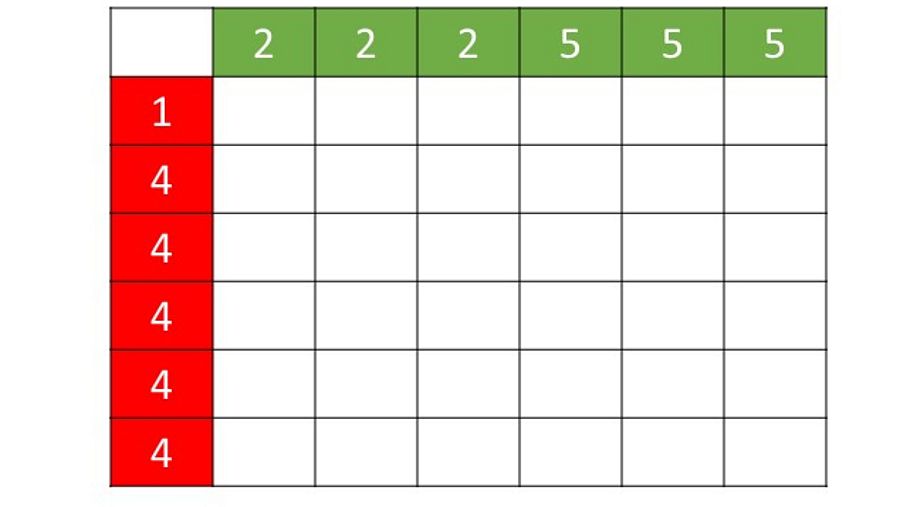
Cómo apuntar los resultados de la partida de dados RTVE

Las celdas interiores de las tablas las coloreamos de ROJO o VERDE en función del color ganador en esa celda. Como cuando jugamos a los barquitos. Si el ROJO saca 1 y el VERDE 2, gana el VERDE. En el cruce de esos 2 resultados, la celda será VERDE. Pero si el ROJO saca 4 y el VERDE 2, gana el ROJO. En el cruce de esos 2 resultados, la celda será ROJO.

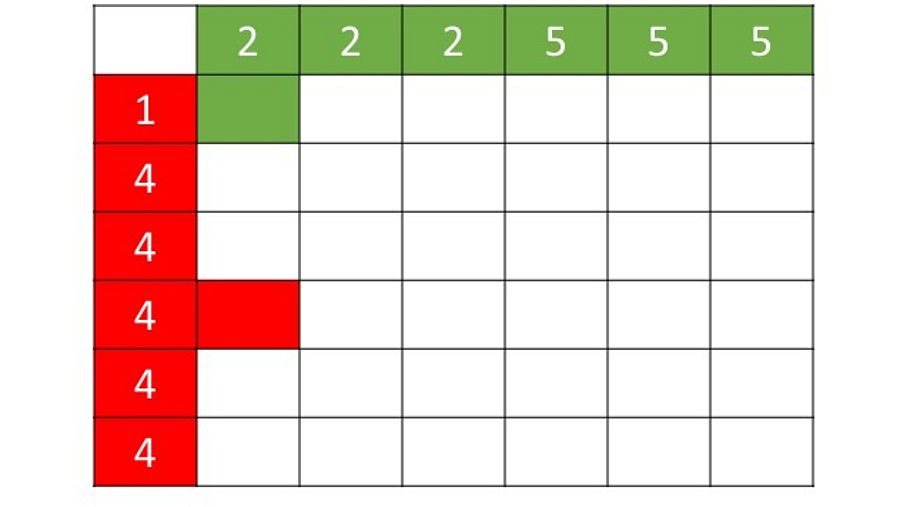
Cómo se apuntan los resultados en una partida de dados RTVE

Cuando terminemos de colorear las 36 celdas, podremos descubrir que hay 21 de ellas verde y solo 15 rojas.

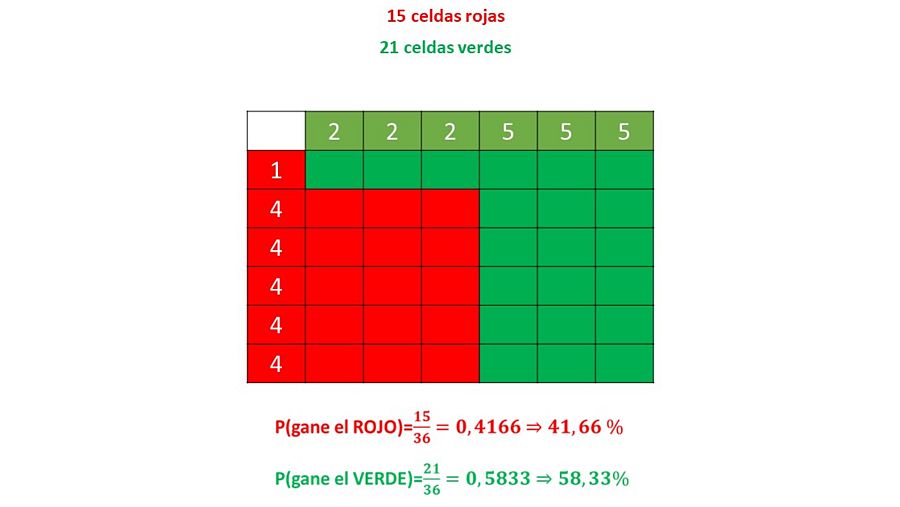
Resultados finales de la partida RTVE

Por lo tanto, podemos concluir que es más probable que gane el dado VERDE. O, dicho de otra manera, el dado VERDE es mejor que el ROJO.

El dado verde tiene más probabilidades de ganar que el rojo RTVE

Si le pido que volvamos a jugar, posiblemente, se sienta tentado (o tentada) de elegir el VERDE. Y está bien. En ese caso, yo elijo el AZUL que, como puede ver en la tabla siguiente, tiene más probabilidades que el VERDE. Podemos concluir que, probabilísticamente, en dado AZUL es mejor que el VERDE.

Probabilidades de ganar en dados no transitivos RTVE

Cálculo de porbabilidades con dados RTVE

Si le pido que juguemos otra vez, posiblemente, elegirá el dado AZUL, ¿verdad? En ese caso, yo elegiré el dado ROJO y ya verá qué sorpresa.

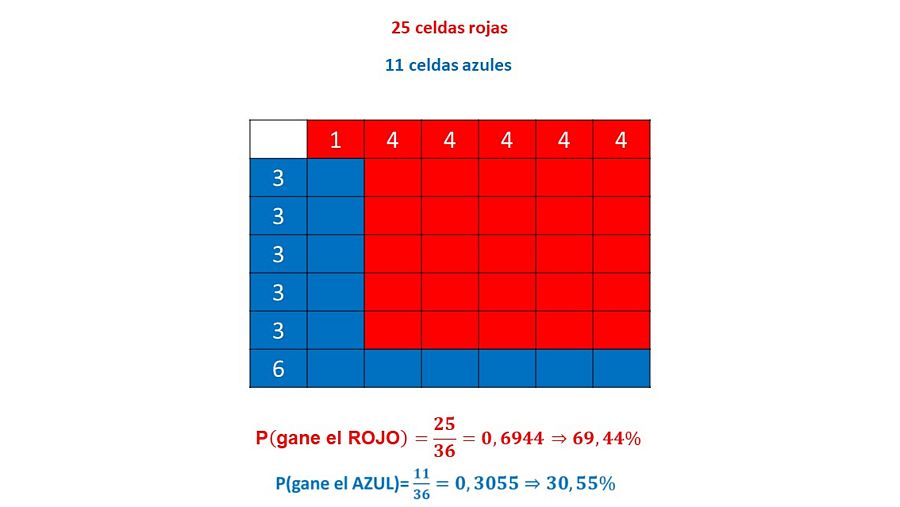
Gana el dado rojo RTVE

Ya ve. El dado ROJO es bastante mejor que el AZUL. Y es que, como ya le dije al principio, estos dados no son transitivos. El AZUL es mejor que el VERDE, el VERDE es mejor que el ROJO pero el ROJO es menor que el AZUL.

Los dados de Clara Grima RTVE

En 'Una matemática viene a verte' nos adentramos en los juegos de azar. RTVE

Y puede ser un ejercicio simpático para jugar con cálculo de probabilidades en Primaria. Se pueden comprar los dados no transitivos, claro, pero también puede encontrar dados blancos más baratos y pintarle los puntos.

De cálculo de probabilidades y juegos de azar hablamos con Gonzalo García Pelayo en el capítulo 7 de Una matemática viene a verte . Con la ayuda de Juan Francisco Navas y Conrado Manuel, ambos de la Universidad Complutense.

* Puedes disfrutar del programa Una matemática viene a verte cada miércoles a las 19:45 horas en La 2 y siempre, cuando quieras -gratis y online- en Una matemática viene a vertemiércoles a las 19:45 horasLa 2RTVE Play.