ACTIVIDADES. PARTE 2
Actividades correspondientes al intervalo del visionado del vídeo: 4 min 12 seg hasta 8 min 34 seg.
Realiza las siguientes actividades tras visonar la parte correspondiente del vídeo.
Las gráficas también nos muestran información sobre la marcha y evolución de un partido de baloncesto. Observa la gráfica y después contesta a las preguntas que tienes debajo.
LA GRÁFICA DEL PARTIDO.
|
a) El tiempo en minutos.
| |
|
b) Los puntos marcados.
| |
|
c) El tiempo que falta de partido.
|
|
a) Las faltas cometidas
| |
|
b)
La diferencia entre los marcadores.
| |
|
c) Los puntos marcados.
|
|
a) Cuál va por delante, la máxima diferencia alcanzada y cuando se ha comenzado a fraguar la victoria.
| |
|
b) Cuál va a ganar, la mínima diferencia y cuál va por delante.
| |
|
c) Quién ha cometido más faltas, cuál va a ganar y cuando.
|
En el vídeo hemos visto cómo la gimnasta lanza la pelota, asciende hasta una altura y vuelve a descender. ¿Podremos conocer cuál es la altura que alcanza? ¿Nos sirven las funciones para conocer ésta información y más?
ESTUDIANDO EL MOVIMIENTO DE LA PELOTA
La ecuación que aparece en el vídeo es: h = 10 t - 5 t2 , que nos indica la
que alcanza la pelota para cada
t. Fíjate como calculan en el
vídeo la altura correspondiente a cada tiempo y contesta:
- Al cabo de 0'5 estará a de altura.
- Al cabo de 1 estará a de altura.
- Al cabo de 2 estará en el .
INVESTIGA CON EL TIRO PARABÓLICO
Accede a la siguiente actividad de Geogebra, donde podrás trabajar con el tiro parabólico. Interactua libremente con la actividad y posteriormente señala las respuestas que sean correctas.
a) Con un ángulo de 41,8º , una velocidad v = 9'28 m/s, se alcanza una altura máxima de 1'95 m pero no se alcanza el objetivo.
| |
b) Con un ángulo de 41,8º , una velocidad v = 9'28 m/s, se alcanza una altura máxima de 1'95 m y se alcanza el objetivo.
| |
EL ORIGEN DE LAS GRÁFICAS.
La representación de una gráfica en el plano es bien sencilla conociendo unas pequeñas reglas. Estas reglas fueron ideadas por dos genios Franceses que, curiosamente no eran Matemáticos profesionales.
LA GENIAL IDEA.
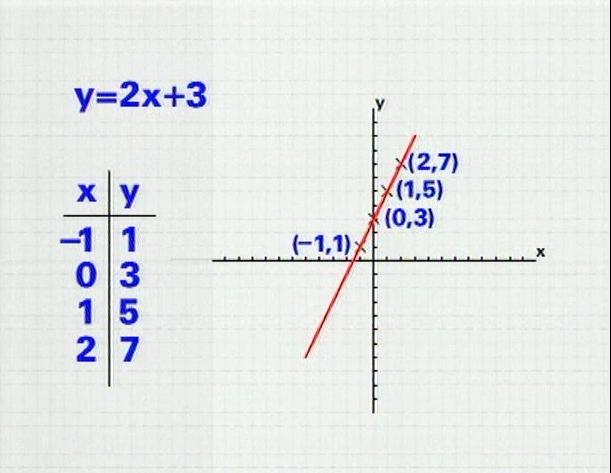
Verdadero Falso
Verdadero Falso
Verdadero Falso
SITUANDO PUNTOS EN EL PLANO.
Practica con la siguiente escena de Descartes, donde puedes ver pasando el ratón las coordenadas de cada punto. Cuando ya lo tengas claro continúa con los ejercicios que encuentras debajo haciendo clic sobre el botón "localiza puntos"