ACTIVIDADES. PARTE 1
Actividades correspondientes al intervalo del visionado del vídeo: desde el comienzo hasta 6 min 02 seg.
Realiza las siguientes actividades tras visonar la parte correspondiente del vídeo.
LA GEOMETRÍA DE EUCLIDES.
1.-
¿Cuál es la geometría de Euclides?
|
a) La geometría de la naturaleza.
| |
|
b) La geometría de las rectas y curvas.
| |
|
c) La geometría del caos.
|
|
a) Para describir el mundo artificial creado por el hombre
| |
|
b) Para describir el mundo natural creado por la naturaleza.
| |
|
c) Para describir los edificios.
|
LA GEOMETRÍA EN LA NATURALEZA.
- Las nubes no son .
- Las montañas no son .
- Las costas no son .
- Las cortezas de los árboles .
- Los relámpagos no se desplazan en .
LA AUTOSEMEJANZA.
En un fractal la forma se va repitiendo a diferentes
escalas dentro del mismo objeto. Esta propiedad que se da en helechos, árboles
y pulmones se llama autosemejanza.
En la siguiente escena de Descartes puedes ver como partimos de un segmento al que vamos repitiendo los mismos cambios en escala. Interactua con la escena libremente.
LA DIMENSIÓN DE UN FRACTAL
Indica de las siguientes afirmaciones cuáles son ciertas o falsas.
Verdadero Falso
Verdadero Falso
CUBRIENDO EL PLANO.
En la siguiente escena de Descartes puedes observar cómo al cambiar el valor de "nivel" la curva se va enrollando más y más hasta cubrir prácticamente una porción de plano.
EL COPO DE NIEVE DE KOCH
Indica cuáles de las siguientes afirmaciones no son ciertas:
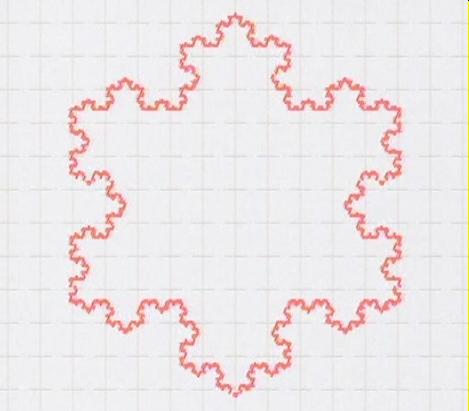
a) Esta curva era conocida desde la antigüedad.
| |
b) Para construirla partimos de un triángulo.
| |
c) Es necesario repetir el proceso de construcción muchas veces para llegar a la curva mostrada.
| |
d) Entre dos puntos del contorno hay infinitos zig-zags.
| |