ACTIVIDADES. PARTE 2

Actividades correspondientes al intervalo del visionado del vídeo: 7 min 21 seg hasta 14 min 31 seg.

 


 

Realiza las siguientes actividades tras visonar la parte correspondiente del vídeo.

Icono de IDevice de pregunta

EL ORIGEN DE PI

 

1.- ¿Cuál es la definición del número Pi?

  
a) Es un número cuyo valor es: 3,14161592...
b) La longitud de una circunferencia por dos veces su radio.
c) Es el cociente entre la longitud de la circunferencia y su diámetro.

 

2.- Arquímedes fue un gran inventor, algunos de sus inventos fueron...

  
a) El tornillo sin fin y las leyes de las palancas.
b) La bañera y el tornillo de los pozos.

 

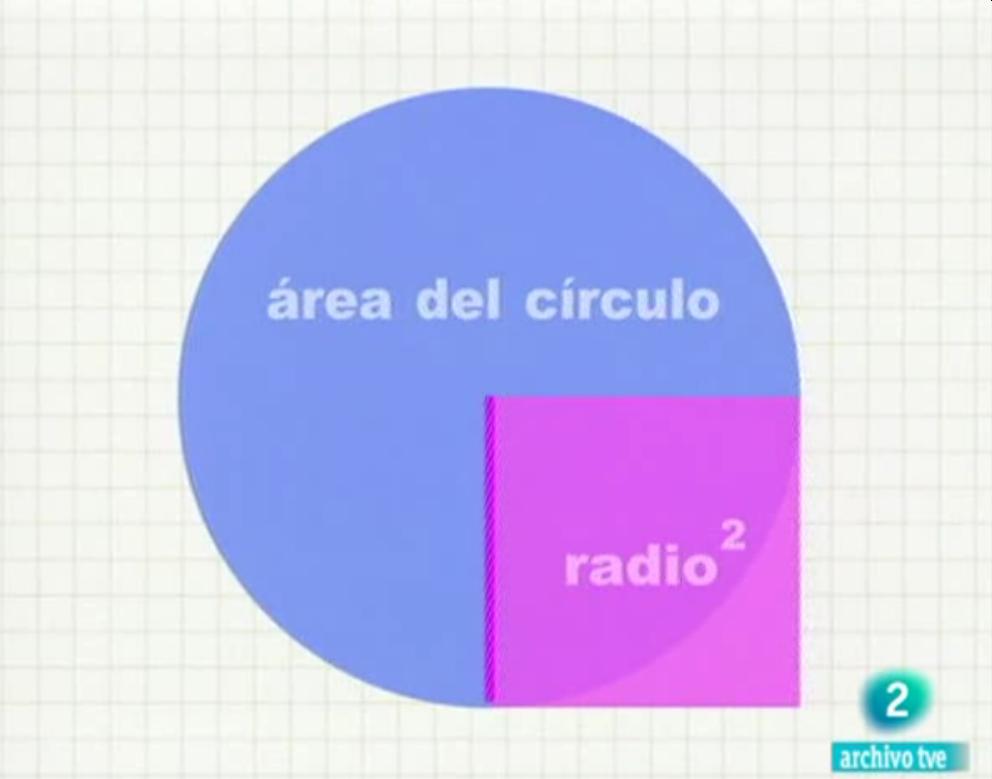
3.- Observa el dibujo, lo hemos visto en el vídeo. ¿Qué relación hay entre estas figuras y el número Pi?

  
a) El cociente entre el área del cuadrado y el área del círculo es una constante igual a Pi.
b) El cociente entre el área del círculo y el área del cuadrado es una constante igual a Pi.
c) Al quitarle al círculo la parte del cuadrado obtenemos Pi.

 
 
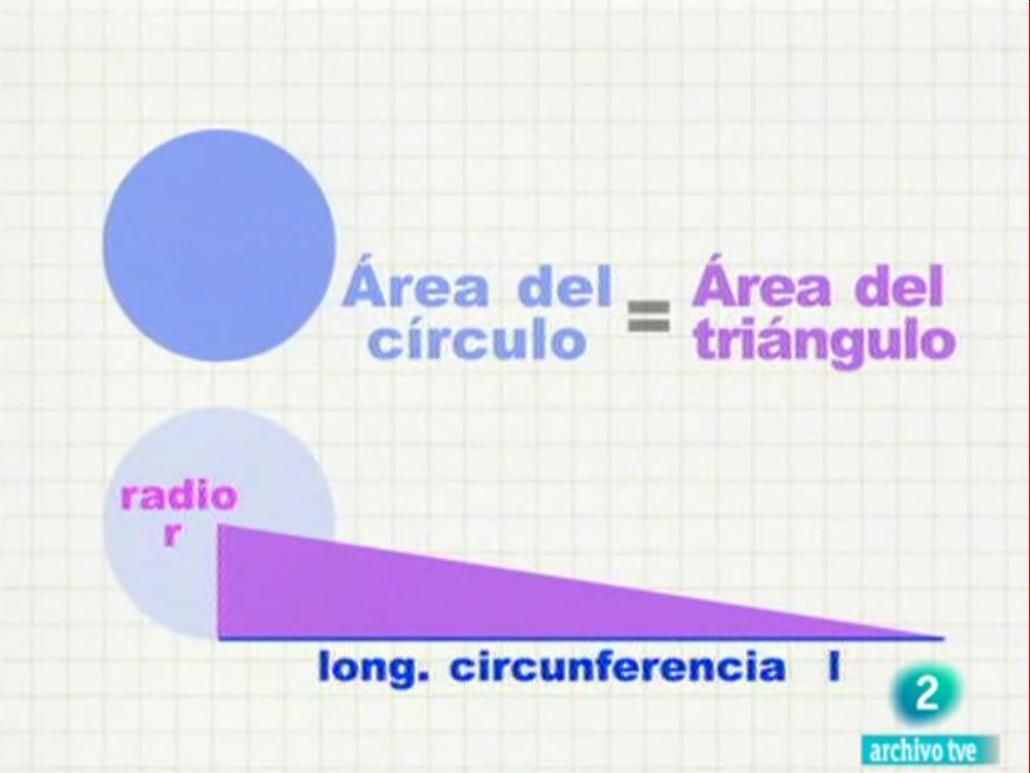
4.- Arquímedes utiliza esta igualdad para demostrar la fórmula del área de un círculo, ¿cuál es de las siguientes?
  
a) Area = Pi · r2
b) Area = 2 · Pi · r
c) Area = Pi · r

Icono de iDevice

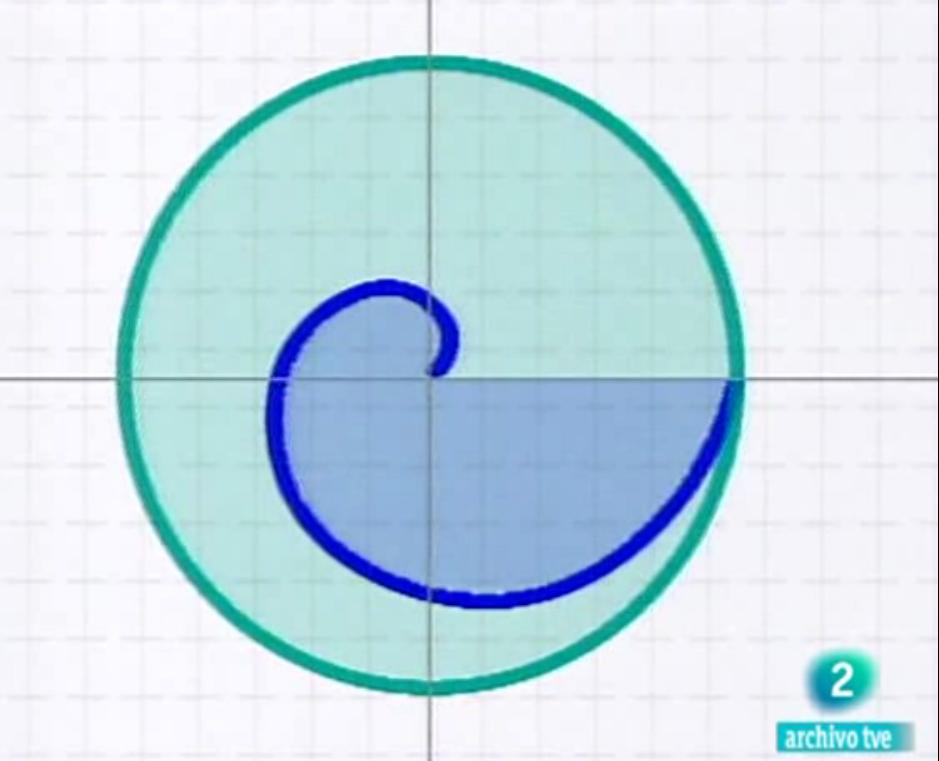
LA ESPIRAL DE ARQUÍMEDES Y EL CÍRCULO

Recuerda la relación que aparece en el vídeo sobre el área que barre la espiral en una vuelta completa y el área del círculo. ¿Sabrías rellenar los huecos?

 


 

 

El área barrida por la en su primera es la parte del del círculo,
cuyo radio es el de esta revolución.
  

CUERPOS REDONDOS.
 
El número Pi es la llave para calcular las áreas y volumenes de todos los cuerpos redondos: Cilindro, Cono, Esfera, troncos de conos. Así como de todas las figuras planas que contengan círculos.

A continuación tienes cuatro escenas de Descartes. Prueba cada una de ellas libremente, aunque aquí tienes algunas indicaciones:

  • La primera escena te permite generar el cilindro como cuerpo de revolución.
  • La segunda escena te permite ver el desarrollo plano del cilindro.
  • La tercera escena te permite generar el cono como cuerpo de revolución.
  • La cuarta escena te permite ver el desarrollo plano del cono.
¡OJO!: En cualquiera de las escenas puedes pinchar con botón izquierdo del raton y arrastrar, para ver girar el cuerpo en el espacio de tres dimensiones.
Esta unidad interactiva requiere la máquina virtual de Java J2RE. Esta unidad interactiva requiere la máquina virtual de Java J2RE.

Esta unidad interactiva requiere la máquina virtual de Java J2RE. Esta unidad interactiva requiere la máquina virtual de Java J2RE.

Escenas extraídas de la unidad: Cuerpos geométricos. Elaborado por José R. Galo Sánchez para el proyecto EDAD

PI Y LOS CUERPOS REDONDOS

Elige entre las siguientes opciones las que son correctas:
Área lateral del cilindro = 2·π · r · h; Area lateral del cono = π · r · g
Área total del cilindro = 2·π · r · h 2· π ·r2; Area total del cono = π · r · g π · r2
Volumen del cilindro = π · r2 · h; Volumen del cono = 1/3 · π · r2 · h
Area de la esfera = 4 · π · r2 ; Volumen de la esfera = 4/3 · π · r3



EL CILINDRO Y EL CONO.

Observa la siguiente actividad de Geogebra. Pulsando y arrastrando los controles puedes ir rellenando ambos cuerpos. Investiga libremente y después contesta a las preguntas que encuentras debajo.

Please install Java 1.4 (or later) to use this page.

Icono de IDevice de pregunta

Pregunta de Elección Múltiple

1.- ¿Cabe la misma cantidad de agua en el cilindro que en el cono?
  
a) Si, exactamente la misma.
b) Casi la misma cantidad.
c) No, el cilíndro se queda sin llenar mientras que el cono ya se encuentra completo.

2.- ¿Qué relación guardan los volumenes de los dos cuerpos? ¿Cuánto se llena el cilíndro con el volumen del cono?
  
a) El volumen del cono llena 1/2 del cilíndro.
b) El volumen del cono llena 1/3 del cilíndro.

« Anterior | Siguiente »