ACTIVIDADES. PARTE 4.

Actividades correspondientes al intervalo del visionado del vídeo: 14 min 49 seg hasta el final.

Realiza las siguientes actividades tras visonar la parte correspondiente del vídeo.

UN ÚLTIMO PROBLEMA

1.- ¿Cuál es el último problema que abordan Newton y Leibnitz?

	a) Calcular el área de figuras curvas.
	b) Calcular el área de una figura limitada por curvas.

2.- ¿Quién fue el primero que intentó calcular el área encerrada por una curva?

	a) Arquímedes
	b) Fermat.
	c) Descartes.

3.- Los rectángulos que dibujamos por debajo de la curva aproximan su suma ...

	a) ... por exceso al área total.
	b) ... por defecto al área total.

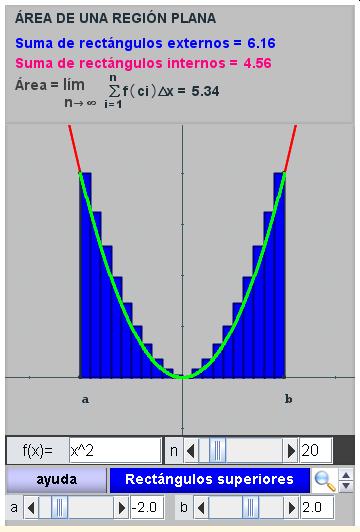
CÁLCULO DE ÁREAS POR EXCESO Y POR DEFECTO.

La siguiente escena permite calcular el área por debajo de una curva en un intervalo (a, b). Puedes cambiar el intervalo, puedes seleccionar los rectángulos inferiores o superiores, puedes aumentar los subintervalos y, también, puedes cambiar la función que quieres representar.

Interactua con la escena libremente, después haz los ejercicios que ves debajo de la escena.

CALCULANDO ÁREAS

Utiliza la escena anterior para calcular las áreas bajo las siguientes funciones.

1.- Escribe como función y = x, pon el intervalo (0, 3) y después mira las áreas por defecto y por exceso. Completa:

Área = JXUwMDZjJXUwMDFhJXUwMDFiJXUwMDA1

para n = 20; suma rectángulos externos = JXUwMDZjJXUwMDFhJXUwMDE5JXUwMDA0 ; suma rectángulos internos = JXUwMDZjJXUwMDFhJXUwMDFjJXUwMDBh

para n = 50; suma rectángulos externos = JXUwMDZjJXUwMDFhJXUwMDFiJXUwMDBj ; suma rectángulos internos = JXUwMDZjJXUwMDFhJXUwMDFhJXUwMDA1

2.- Escribe como función y = x², pon el intervalo (-2, 2) y, después mira las áreas por defecto y por exceso. Completa:

Área = JXUwMDZkJXUwMDFiJXUwMDFkJXUwMDA3

para n = 50; suma rectángulos externos = JXUwMDZkJXUwMDFiJXUwMDE4JXUwMDAw ; suma rectángulos internos = JXUwMDZkJXUwMDFiJXUwMDFlJXUwMDAy

para n = 80; suma rectángulos externos = JXUwMDZkJXUwMDFiJXUwMDFiJXUwMDAx ; suma rectángulos internos = JXUwMDZkJXUwMDFiJXUwMDFmJXUwMDA1

TEOREMA FUNDAMENTAL DEL CÁLCULO INTEGRAL

De las siguientes frases di cuáles son verdaderas y cuáles falsas.

1.- Trabajando con las integrales, Newton y Leibnitz llegarón a la conclusión de que la derivada de la función área es la función que hemos integrado.

Verdadero Falso

2.- Newton era más famoso en su época que Einstein en el siglo XX.

Verdadero Falso

3.- Leibnitz fue tan famoso como Newton.

Verdadero Falso

4.- Los cráteres de Newton y Leibnitz que se encuentran en la Luna están muy próximos.

Verdadero Falso