MOVIMIENTOS
ACTIVIDADES. PARTE 3
Actividades correspondientes al intervalo del visionado del vídeo: 8 min 00 seg hasta el final.
Realiza las siguientes actividades tras visonar la parte correspondiente del vídeo.
DE FRISO A MOSAICO.
Ya hemos visto cómo decorar nuestras paredes con un friso. Ahora nos extendemos en el plano para conseguir cubrir nuestros suelos. Observa la siguiente escena de Descartes, partiendo de una figura de las cuatro que tenemos y utilizando la traslación obtenemos un friso. Si después continuamos rellenando el plano conseguimos un mosaico.
Escena extraída de la unidad didáctica: Movimientos en el plano. Realizada por José Mª Aína Martínez, para el proyecto EDAD
TRABAJANDO CON MOSAICOS REGULARES
Según hemos visto en el vídeo: "Un mosáico periódico es el que rellena todo el plano mediante la repetición de una misma forma o motivo elemental." ¿Podemos rellenar el plano con cualquier polígono regular? Contesta una a una las siguientes preguntas.
1.- Los únicos polígonos regulares que nos permiten cubrir el plano son: El triángulo equilátero, el cuadrado y el hexágono.
Verdadero Falso
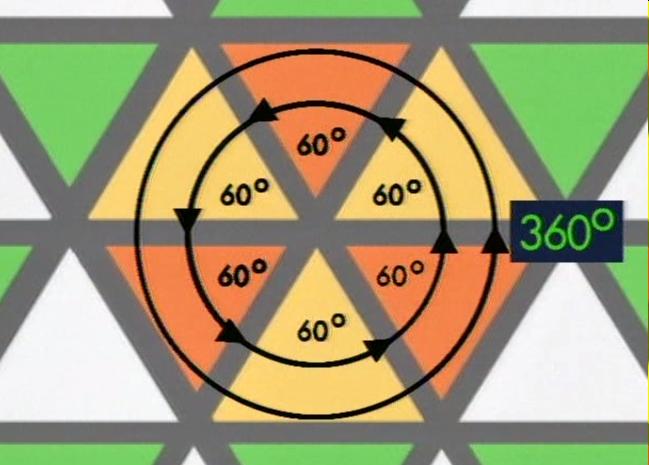
2.- Que sólo podamos cubrir un plano con triángulos, cuadrados o hexágonos, es debido a que en cada vértice confluyen ángulos cuya suma es 300º.
Verdadero Falso
CONSTRUYENDO MOSAICOS REGULARES.
Si sólo es posible cubrir el plano con triángulos, cuadrados y hexágonos, parace que nuestros suelos van a quedar muy simples. Sin embargo, no es así. Utilizando la imaginación y el color cambiará considerablemente el diseño de nuestros suelos. Aquí tienes dos ejemplos que tienes que hacer con la actividad de Geogebra que tienes debajo.
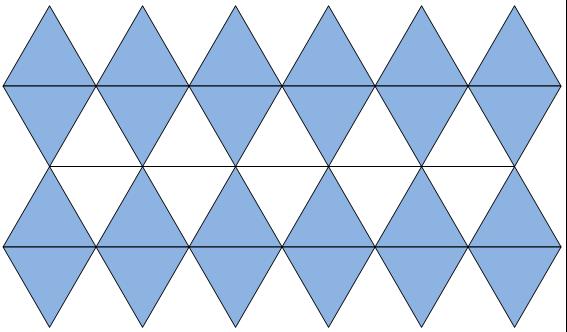
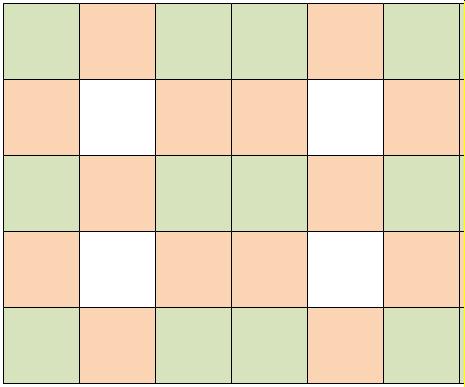
En la barra de herramientas tienes el último botón . Haciendo clic sobre el pequeño triángulo que aparece en la esquina inferior derecha, se despliega un menú donde puedes seleccionar los triángulos o cuadrados que necesites. Cada uno de ellos aparece, además, con ocho colores diferentes. Para dibujar un polígono tienes que señalar dos puntos, que serán los vértices de uno de sus lados. Has de tener en cuenta que según el orden en que señales los puntos hay dos orientaciones posibles, de las cuales una será la deseada y la otra no.
. Haciendo clic sobre el pequeño triángulo que aparece en la esquina inferior derecha, se despliega un menú donde puedes seleccionar los triángulos o cuadrados que necesites. Cada uno de ellos aparece, además, con ocho colores diferentes. Para dibujar un polígono tienes que señalar dos puntos, que serán los vértices de uno de sus lados. Has de tener en cuenta que según el orden en que señales los puntos hay dos orientaciones posibles, de las cuales una será la deseada y la otra no.
Actividad de Geogebra: Mosaicos regulares e irregulares. Realizada por Rafael Losada Liste y José Luis Álvarez García, para el proyecto Gauss.
MOSÁICOS SEMIRREGULARES.
1.-Para construir este tipo de mosáicos utlizamos: ...







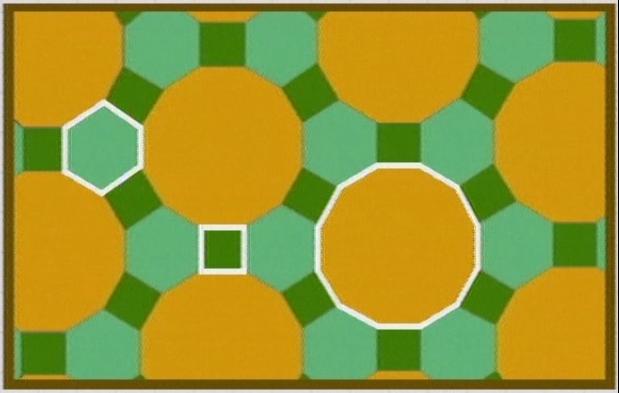
Elige uno y dibujalo con la actividad de Geogebra anterior.
|
a) ... triángulos equiláteros, cuadrados o hexágonos, de modo que la suma de los ángulos de los que confluyan en un mismo vértice sea 360º.
| |
|
b) ... triángulos equiláteros, cuadrados o hexágonos cuyos lados miden cualquier longitud.
|