ACTIVIDADES. PARTE 3

Actividades correspondientes al intervalo del visionado del vídeo: 10 min 32 seg hasta 16 min 12 seg.

 


 

Realiza las siguientes actividades tras visonar la parte correspondiente del vídeo.

LIBRO DE ANOTACIONES DE GAUSS

Las siguientes frases son verdaderas o falsas. Elige tu opción.


1.- Gauss anotaba sus descubrimientos en un pequeño cuadernillo, que llevaba siempre consigo.

Verdadero Falso


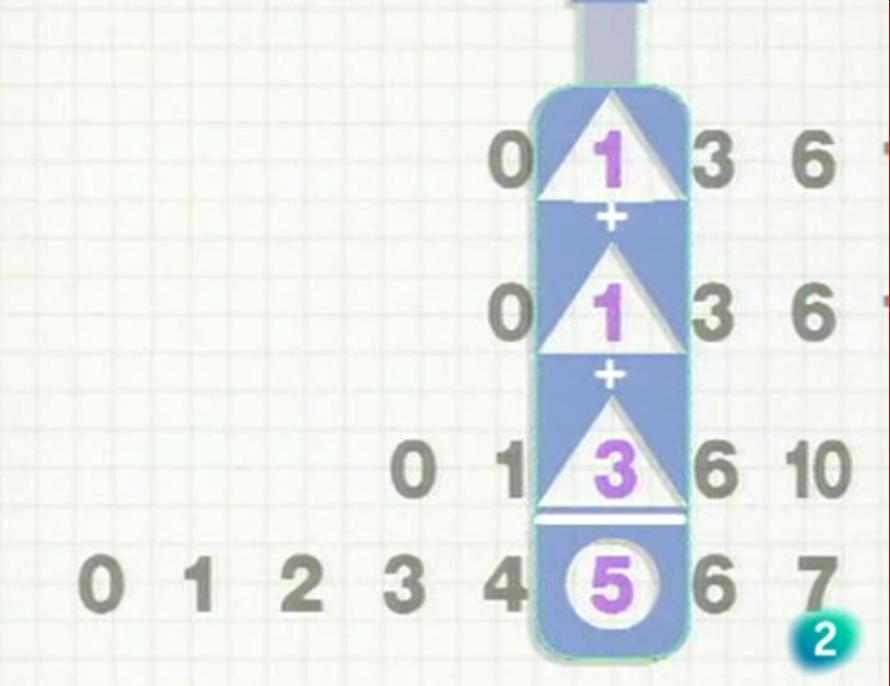
2.- Una de las anotaciones en el cuadernillo de Gauss fue:


Que es un resultado que tiene que ver con la construcción de triángulos.

 


Verdadero Falso
Icono de IDevice de pregunta

RESOLVIENDO ECUACIONES.

Gauss nos mostró que cada ecuación tiene tantas soluciones como nos indica...
  
a) ... el número de términos de la ecuación.
b) ... el grado de la ecuación.
c) ... el término independiente de la ecuación

2.- Al resolver a ecuación x - 2 = 3. Obtenemos como solución:

  
a) x = 5
b) x = 1

2.- Resuelve la ecuación de 2º grado: 3x2 - 4x 1 = 0. Las soluciones son: (Puedes ayudarte de la escena que ves más abajo)
  
a) x = 1/3; x = 1
b) x = -1; x = -1/3

TRABAJANDO CON ECUACIONES POLINÓMICAS

Las ecuaciones no sólo se pueden resolver con números (algebraicamente), también puede obtenerse su solución a través de su gráfica (geométricamente). En la siguiente escena de Descartes puedes representar la gráfica que se corresponde con la ecuación que quieras resolver.

Por ejemplo, La que aparece por defecto nos permite resolver la ecuación: 3x2 - 4x 1 = 0. Observa que las soluciones de dicha ecuación coinciden con los puntos de corte de su gráfica con el eje X.

Para calcular otras ecuaciones sólo tienes que cambiar la ecuación. Interactua libremente con la escena y después resuelve las ecuaciones que te piden.

Instrucciones:

1.- Para cambiar la función haz clic en el cuadro donde aparece la función y borra lo que quieras, modificando o añadiendo.

2.- Puede ser que necesite elevar al cuadrado, al cubo, tienes que teclear mayúsculas y la tecla al lado de la tecla P. ^

 

Esta unidad interactiva requiere la máquina virtual de Java J2RE.

Escena adaptada  por Eva M Perdiguero. Extraída de: La ecuación de segundo grado. Realizada por Leoncio Santos Cuervo
Icono de IDevice de pregunta

RESOLVIENDO ECUACIONES GRAFICAMENTE.

1.- Resuelve la ecuación: x3 - 3x2 - x 3 = 0 (Utiliza la escena para representar su función)
  
a) x = - 2, x = 1, x = 3
b) x = 1, x = -1, x= 3
c) x = 2, x = - 1, x = - 3

2.- Resuelve la ecuación: x2 - 4x 4 = 0
  
a) x = 2, (doble)
b) x = 2; x = -2

LOS NÚMEROS COMPLEJOS.

La raíz del número -1 no tiene solución, a dicho número se le llamó i y así nacieron unos nuevos números llamados complejos.

√-1 = i

Como este número no cabía en la recta de números reales, Gauss inventó el eje imaginario perpendicular al eje de la recta real.

CONOCIENDO LOS NÚMEROS COMPLEJOS

Selecciona las opciones que son ciertas, entre las siguientes:
Para representar los números complejos utilizamos dos ejes, en el horizontal representamos la parte real y en el vertical la parte imaginaria.
Los números complejos nos permiten resolver ecuaciones como x 3 - 8 = 0.
Gracias a Gauss los números complejos cobraron sentido en la comunidad matemática que los aceptó.



« Anterior | Siguiente »