ACTIVIDADES. PARTE 1
Actividades correspondientes al intervalo del visionado del vídeo: 0 min 0 seg hasta 6 min 44 seg.
Realiza las siguientes actividades tras visonar la parte correspondiente del vídeo.
FRASES CÉLEBRES.

Si hubiese que los cuatro matemáticos más de la historia,
seguramente sería uno de ellos, junto a , y .
EL GRAN EULER.
1.- De los cuatro matemáticos antes nombrados, ¿cuál fue el más prolífico en obras matemáticas?
|
a) Arquímedes.
| |
|
b) Euler.
| |
|
c) Newton.
| |
|
d) Gauss.
|
|
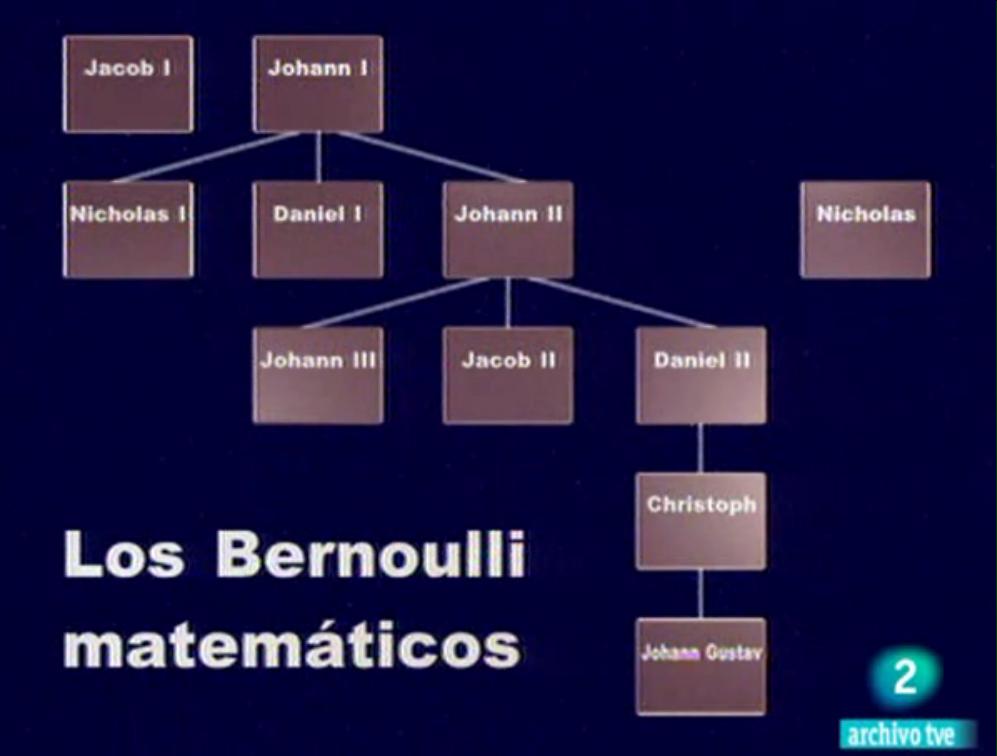
a) La familia Bernoulli. | |
|
b) Los pitagóricos. | |
|
c) Los Newton. |
3.- ¿Qué otros estudios tenía Euler?
|
a) Sólo sabía Matemáticas.
| |
|
b) Estudió: Teología, Astronomía, Medicina, Física y Lenguas orientales.
| |
|
c) Estudió: Medicina, Astrología, Filosofía y Lenguas clásicas. |
LOS PUENTES DE KÖNIGSBERG
Königsberg era una ciudad de la antigua Prusia, situada a orillas del Báltico. Estaba atravesada por el río Pregel que la divide en cuatro partes, conectadas entre sí por siete puentes. Los vecinos se preguntaban cuál sería la ruta para atravesar los siete puentes pasando sólo una vez por cada uno. Euler demostró que era imposible, dando origen a una nueva rama de las matemáticas: la teoría de grafos.
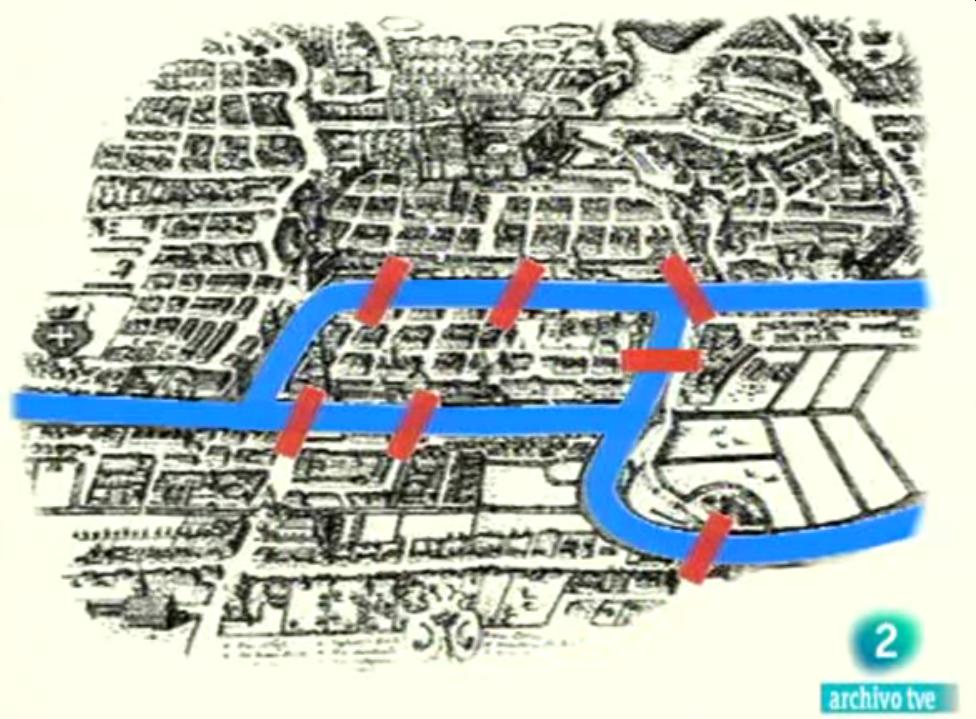
¿QUÉ PASARÍA SI HUBIERA 8 PUENTES?
LA SOLUCIÓN DE EULER A LOS PUENTES.
Euler demostró que para que el problema de los puentes tuviera solución cada punto tendría que tener un nº par de caminos, salvo el de partida y el de llegada.
| |
En el esquema que utilizó Euler cada parte de la ciudad conectada era un punto y cada puente una línea que comunicaba dos partes de ciudad.
| |
La teoría de grafos hubiera surgido independientemente del número de puentes que había en la ciudad.
| |
LA OBRA DE EULER.

Verdadero Falso
Verdadero Falso