ACTIVIDADES. PARTE 3

Actividades correspondientes al intervalo del visionado del vídeo: 10 min 32 seg hasta 16 min 31 seg.

DIVISORES DE UN NÚMERO.

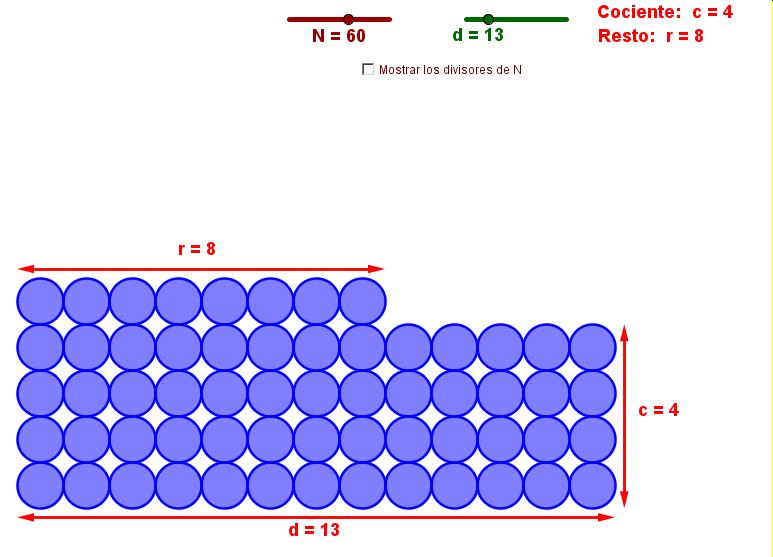
Para calcular los divisores de un número vamos dividiendo el número entre 2, 3, 4, 5, 6, ... y si el resto de la división es cero, entonces el número por el que hemos dividido es divisor del primero. Por ejemplo: los divisores de 10 son: 1, 2, 5, 10. Cuando dividimos 10 : 2 nos da de cociente 5 y resto 0. Por lo tanto, 2 es divisor de 10.

En la siguiente actividad puedes ir calculando los divisores del número que quieras entre 1 y 100. Prueba a cambiar el número N a 12 y buscar sus divisores. Observa qué ocurre con las figuras que van formando los círculos inferiores. Despues realiza las actividades propuestas.

Un número es primo cuando no tiene más divisores que la unidad y el mismo. Cuando un número no es primo se dice que es compuesto.

Ejemplos:

5 es primo porque sólo es divisible por 1 y 5.

10 no es primo, porque es divisble por 1, 2, 5 y 10.