ACTIVIDADES. PARTE 4

Actividades correspondientes al intervalo del visionado del vídeo: 16 min 31 seg hasta el final.

Realiza las siguientes actividades tras visonar la parte correspondiente del vídeo.

Icono de iDevice

LAS SERIES INFINITAS.

Euler, a pesar de quedarse ciego, siguió escribiendo dictándole a uno de sus hijos. Completa las siguientes series que has visto en el vídeo:

 

1 1/2 1/ 1/8 /16 ......... =

 

 

1 1/ 1/3 1/ 1/5 ........... = ∞

 

 

1 1/ 2 1/ 2 1/ 42 .......... = π2/

 

 

1/ 1/16 1/ 1/64 ....... = π2/

 

 

1 1/ 1/ 1/49 ......... = π2/

 


  

ALGUNAS SUMAS.

Aquí tienes una calculadora con la que podrás realizar las sumas que te planteamos a continuación. Por aproximación escoge la solución que más se acerque al resultado que has obtenido.

 

Haz clic sobre la calculadora para usarla

¿CUÁL ES EL RESULTADO?

Ves haciendo las sumas término a término, para ver hacia donde tiende la suma total


1.-El valor de la suma  - 9 3 -1 9/27 -9/81 9/243 = ... es aproximadamente -6

Verdadero Falso


2.- El valor de la suma, -8 - 16/3 - 32/9 - 64/27 - 128/81 - 256/243 - 512/729 - 1024/2187 - 2048/6561 es .... de forma aproximada -24

Verdadero Falso


3.- El valor de la suma, -3 3/2 - 3/4 3/8 - 3/16 3/32 es ... de forma aproximada -2

Verdadero Falso

LOS NÚMEROS COMPLEJOS.

La raíz del número -1 no tiene solución, a dicho número se le llamó i y así nacieron unos nuevos números llamados complejos.

√-1 = i

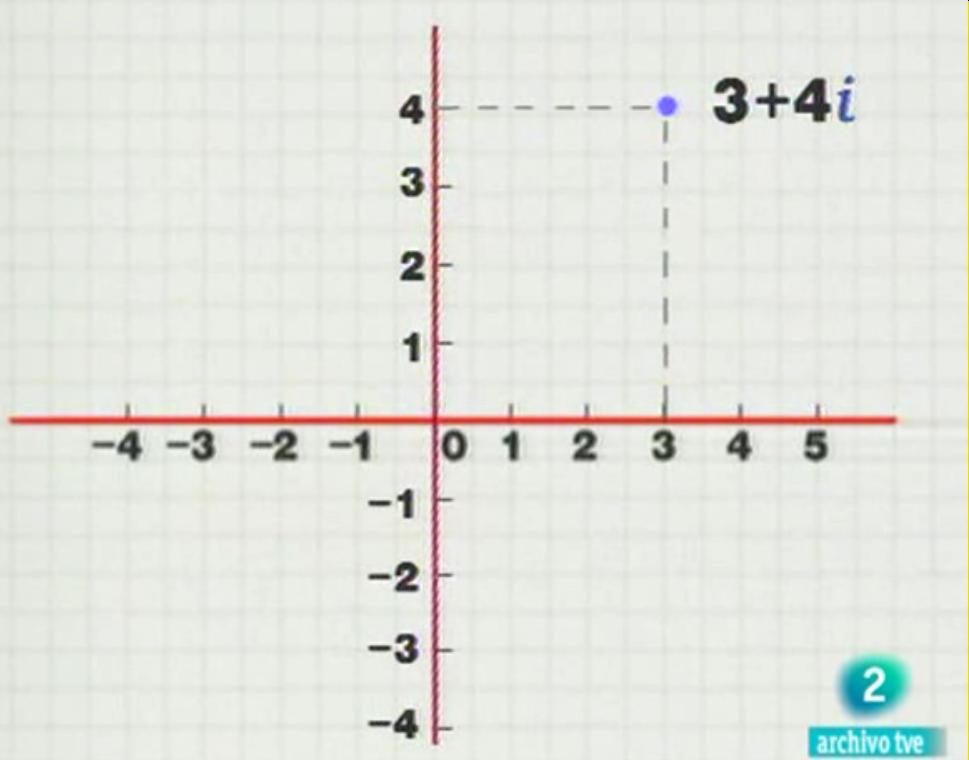
Como este número no cabía en la recta de números reales,

Gauss inventó el eje imaginario perpendicular al eje de la recta real.

Icono de IDevice de pregunta

LOS NÚMEROS PROTAGONISTAS DE LA PELÍCULA.

1.- ¿Qué número emblemático aparece de forma sistemática en muchas de las sumas de las series de Euler?
  
a) El nº e.
b) El nº Pi = π
c) El nº 1.

2.- ¿Donde aparece el nº e?
  
a) En el crecimiento de epidemias, en los cables de las lámparas,...
b) En el crecimiento de una epidemia, en la prueba del carbono 14 y en los cables de alta tensión de la luz.
c) En el crecimiento de nuestra medida, en la prueba de carbono 17 y en los cables.

3.- ¿Cuál es la relación entre todos los números: 0, 1, Pi, e, i?
  
a) eiπ 1 = 1
b) eiπ 1 = 0
c) eiπ 0 = 1

« Anterior | Siguiente »